Cart-Ramp Investigation

INTRODUCTION

This experiment uses a ramp and a low-friction cart. As the cart rolls down a ramp, it builds up speed – accelerates. Using a photogate, we will investigate the pattern by which the speed (velocity) increases. In the process we will learn more about some of the features of Logger Pro software.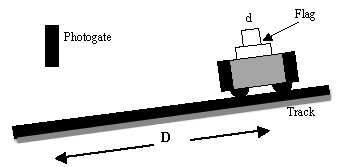

Figure 1

OBJECTIVES

* Collect data as a cart rolls different distances down an inclined plane
* Analyze the graph of time (Dt) vs. distance (D) for the cart
* Analyze the graph of velocity (v) vs. distance for the cart

MATERIALS

computer
Vernier Photogate
Vernier computer interface
Vernier Dynamics System
Logger Pro
Flag cut from Index Card

PRELIMINARY QUESTIONS

1. Sketch your prediction for the speed vs. distance graph as the cart rolls down the ramp. Describe in words what this graph means.
2. How would your predicted graph change if you changed the angle of the incline? Explain.

PROCEDURE

1.   Set up the equipment as illustrated in Figure 1. Make the “flag” from an index card, making the top 2.0 cm wide (d). Tape it to the side of the cart.

2.   Adjust the photogate so the flag on the moving cart will move through it and cause the LED indicator to turn on as it goes through.

3.   Connect the photogate to the interface and then connect to the computer. Launch Logger Pro. A default file should open up ready to collect data with the attached photogate.

4.   Click on File > Open > Probes & Sensors > Photogates. Then open the file “Gate vs Event.cmbl”

5.   In the window labeled “PhotogateDistance1”, double-click and change the value from 0.1 m to 0.02 m, the width of your flag.

6.   Place the cart on the track near the bottom with the leading end at a specific position. Move the photogate so it is at the front edge of the flag. The LED on the photogate will light up when the flag just eclipses the beam. Mark this position with a piece of masking tape if necessary.

7.   Move the cart so it’s distance D from the position you identified in Step 4 is 10 cm up the inclined track*. Start data collection. Release the cart so it moves down the track and through the photogate. Note the Gate Time and Velocity in the Data Table included in these instructions along with the distance (D).

8.   Repeat your run at the 10-cm distance three times and compare your results. Are they consistent? Why or why not? Once you have perfected your procedure, you may not need to do repeated trials at the other distances.

9.   Move the cart up the inclined track in 10-cm increments, noting the three data values each time you make a data run. Once you obtain 5-10 sets of data points, stop data collection. Go on to ANALYSIS.

ANALYSIS

1.   In Logger Pro, start a new file (File > New). Don’t save your data from the previous experimentation.

2.   Enter the data from your data table. Double-click at the top of each table, entering the labels and units for each.

3.   The first graph that will appear will be Gate Time vs Distance. In general, how did the time for the cart to go through the photogate change as you increased the distance it moved? Would you characterize this as a “direct” or an “inverse” type of relationship?

4.   Click and drag across your data points then choose Analyze > Curve Fit from the main menu bar. If you think the data is a “direct” relationship, try fitting it with Linear. Click the button next to “Linear” then click [Try Fit]. If you think it is “inverse”, scroll down to the choice “Inverse”, click the button, then [Try Fit]. You can also try “Inverse Square”. How did your curve fitting go?

5.   Cancel out of the curve fitting. Click on the y-axis label (Gate Time). In the menu that appears, choose “Velocity”. Click on the Autoscale button -

6. In general, how does the velocity of the cart change as you increased the distance it moved? Would you characterize this as a “direct” or an “inverse” type of relationship?

7. Click and drag across your data points then choose Analyze > Curve Fit from the main menu bar. If you think the data is a “direct” relationship, try fitting it with Linear. Click the button next to “Linear” then click [Try Fit]. If you think it is a curve of some sort, try some of the other options. If you think it’s an “inverse” relationship, scroll down to the choice “Inverse”, click the button, then [Try Fit]. You can also try “Inverse Square”. How did your curve fitting go? We’ll return to this analysis below.

DATA TABLE

Distance (D) m	Gate Time (t) s	Velocity (v) m/s

FURTHER ANALYSIS

1.   By now you likely think the velocity vs distance is a direct type of relationship. But a linear fit doesn’t work while a quadratic fit seems to work pretty well. Let’s proceed on this assumption a bit. If a quadratic fit works and if the values for B and C are small, the key determiner of the relationship is the coefficient A and the variable is v². What we would like to do is plot velocity squared vs distance to see if we are correct.

2.   Go to Data > New Calculated Column. Label it “Velocity Squared”, short name: “v^2”, and units of “m^2/s^2” (or m²/s²). In the Expression space, use the drop-down menu for “Variables” to obtain “velocity”. Then add: “^2” to create “velocity”^2 as your expression. This will square every value of velocity and create a new column in the data table. Do not type in the variable – choose it from the menu. Click on [Done] to finish this step.

3.   On the graph of velocity vs distance, click on the y-axis label. On the menu that appears, click on “Velocity Squared”. How does your data look now? Is it linear? How could you test? If it is linear, then you know the relationship is v² a D. One way to express this is to say, “As the distance doubles, the velocity increases four times.”

4.   Velocity (speed) is distance divided by time or d/Dt. Develop an argument for why doing an inverse square fit for Gate Time vs Distance yields a good straight line fit.

Cart on a Ramp Investigation