CAPACITOR CHARGE/DISCHARGE 1 - LQ
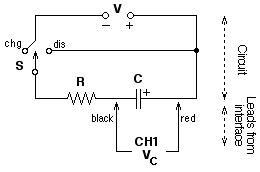
PURPOSE
The purpose of this lab is to examine the pattern of voltage vs. time for charging and discharging capacitors. In the process, you will examine the mathematical equation that describes the data.

CIRCUIT

MATERIALS
50-mF Capacitor, 47-KW Resistor, 1.5-volt cell with holder, SPDT Switch, Wires, Vernier Voltage Probe, Vernier LabQuest, LabQuest App., extra capacitors and resistors

PROCEDURE

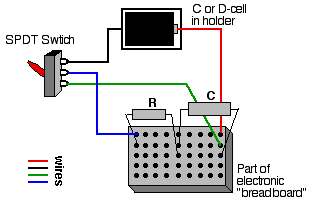
  1. Set up the circuit as shown above using a 50-mF capacitor and 47-KW resistor. Pay attention to the polarity of the voltage source and the capacitor. The switch (S) can be a mechanical switch or simply a place where you can complete the circuit by connecting wires. (This can easily be set up on a breadboard. See diagram below.)
  2. Connect the Voltage Probe to Channel 1 (CH1) on the LabQuest. Then connect the leads to the circuit, being careful to have the leads connected as diagrammed. Launch LabQuest App. Tap on the Data Collection box on the right-hand side of the Sensor screen. Set the data collection as follows:
    Mode: Time Based Length: 15 seconds Rate: 20 samples/second

    CHARGING:

  3. Before charging the capacitor, move the switch to the position labeled "dis". Monitor the voltage and when it reaches 0.0, you may begin this portion of the data collection. [To hurry the discharge along, touch the two ends of a piece of wire to the terminals of the capacitor and tap the sensor space on the Setup screen. Choose Zero from the menu.]
  4. Press the Collect button on the front or tap the Collect icon on the screen to start data collection. At the same time, move the switch to the "chg" position.
  5. At the end of data collection, sketch and describe the shape of this graph. Put into words what is happening inside the capacitor.
  6. Tap the box with the file cabinet icon. This stores your charging run and readies LabQuest to collect a second run.

    DISCHARGING:

  7. With the capacitor fully charged, press the Collect button or tap the Collect icon to start data collection. At the same time, move the switch to the "dis" position.
  8. Sketch and describe the shape of the graph.
  9. Go to the ANALYSIS section.
  10. Try other resistor-capacitor combinations as time permits, obtain the new components from the instructor. See Extensions.

 

ANALYSIS

  • DISCHARGING:
    •
    1. Select a section where the graph is curving smoothly by tapping and dragging with the stylus. Complete a curve fit operation using a "Natural Exponent" regression.
    2. The software evaluates the data for an equation of the form y = A e-Ct + B. Record the value C for the exponent.
    3. Calculate the product of the resistance R and the capacitance C. Then take the inverse product of this value, (RC)-1.
    4. The mathematical equation that describes the voltage on a discharging capacitor is . Note that the constant C that we calculated should be equal to the reciprocal of the RC product. Compare the inverse to the value of the exponent in your equation by calculating the percent difference. How does this difference compare to the tolerances for the resistor and for the capacitor?
    5. Return to the procedure and complete the discharge portion of the lab. Evaluate the resulting graphs using the same procedure as before, except focus on the capacitor voltage VC versus time.

    DATA

    Resistance, R

     

    Capacitance, C

     

    Exponent, C

     

     

    Product, RC

     

     

    Inverse RC, (RC)-1

     

     

    % Difference

     

     

    MORE ANALYSIS

    1. If we examine the general equation for exponential decay, we could substitute the value Vo/2 for V(t), and solve for the time it takes for the voltage to drop to half its former value.
      V(t) = Vo/2 = Vo e-t/RC

      1/2 = e-t/RC

      ln (1/2) = -t/RC

      t1/2 = -RC ln (1/2) = 0.693 RC

    2. Now go to your data for the capacitor voltage during discharge. Pick a value for voltage near the highest one and record the voltage and time in the following table. Then scroll down until you get to a voltage that’s approximately half of that. Record these new values. Repeat, going down in halves.
    1. Voltage
      Time
      t1/2

       

       

       

       

       

       

       

       

       

       

       

       

       

       

       

      1. Subtract the first time from the second, the second from the third, etc. to yield the half-voltage time. When finished, calculate the average half-voltage time.
      2. What you have just done is to demonstrate that capacitors discharge in a mathematical pattern that is identical to the half-lives that radioactive materials demonstrate. Namely, that in equal times, half of the original decays away, then in an additional equal time, half of that decays. And right there on your lab bench!
      3. Compare the average time your capacitor took to drop to half its voltage value with the theoretical 0.693 RC. How does the percentage difference compare to the tolerances of the resistor and capacitor?

       

      EXTENSIONS

      1. Explore using different capacitor values and different resistor values. What happens to the shape of the graph and the resulting constant if you use a larger value for each.
      2. Put two resistors in series and repeat the experiment. Is the resulting graph the result of a larger or a smaller resistance? Repeat with the two resistors in parallel. What do you conclude about how the resistor values "total" when connected in these two ways?
      3. Put two capacitors in series and repeat the experiment. Is the resulting graph the result of a larger or a smaller capacitance? Repeat with the two capacitors in parallel. What do you conclude about how the capacitance values "total" when connected in these two ways?

      CIRCUIT

      1. The following pictorial diagram shows one way that this lab can be carried out easily. The parts can be stored in a small space and can be used in part with other circuit labs. A DPDP switch could be substituted, or even a SPDT knife switch.

       

      Click here to download this lab in MS Word format - capacito1-LQ.doc

      Click here to download this lab in pdf format - capacito1-LQ.pdf

       

      C. Bakken
      November 2007